الشبكة المغزلية
المزيد من الإجراءات
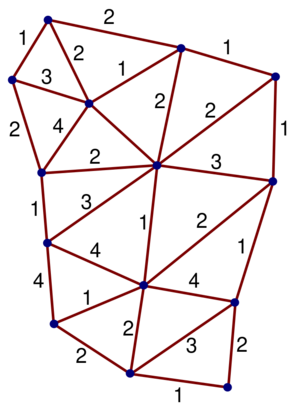
الشبكة المغزلية في الفيزياء (بالإنجليزية: Spin network) هي وسيلة رسومية لتمثيل حالات وتفاعلات الجسيمات والحقول في الميكانيكا الكمية. وهي وسيلة موجزة من منظور رياضي لتمثيل الدوال متعددة الخطية والوظائف بين تمثيلات مجموعات المصفوفة. وبالتالي، فهي أداة قوية يمكن استخدامها لتبسيط العمليات الحسابية.
وصف عالم الفيزياء روجر بنروز الشبكة المغزلية في عام 1971،[1] وهي بنية رياضية شكلت أساسًا لنظرية الجاذبية الكمومية التي طبقها في بعد عالم الفيزياء النظرية كارلو روفيلي، وعالم الفيزياء النظرية لي سمولين، وعالم الفيزياء النظرية جورج بولين، والفيزيائي رودولفو جامبيني وغيرهم من العلماء.
تعريف الشبكة المغزلية
تعريف بنروز
الشبكة المغزلية، كما وصفها بنروز عام 1971،[1] هي نوع من التخطيط البياني يمثل فيه كل قطعة خطية خط العالم (وصف لمسار الجسم في الزمكان النسبي) لـ"وحدة" (إما جسيمًا أوليًا أو نظام مركب من الجسيمات). تنضم ثلاثة مقاطع خطية عند كل رأس. يمكن تفسير الرأس على أنه حدث فيه إما انقسام وحدة واحدة إلى اثنتين أو اصطدام وحدتين واندماجهما في وحدة واحدة.
تسمى الرسوم البيانية التي ترتبط فيها جميع مقاطعها الخطية بالقمم بالشبكات المغزلية المغلقة. يمكن اعتبار الزمن يسير في اتجاه واحد، مثل من أسفل إلى أعلى الرسم البياني، ولكن بالنسبة للشبكات المغزلية المغلقة فإن اتجاه الوقت غير ذي صلة بالحسابات.
يمكن حساب عدد صحيح غير سالب يسمى معيار الشبكة المغزلية في كل شبكة مغزلية مغلقة. يمكن استخدام هذه المعايير لحساب احتمالات قيم المغزل المختلفة.الشبكة التي يكون معيارها صفراً لها احتمالية حدوث مساوية للصفر. تقع القواعد الخاصة بحساب المعايير والاحتمالات خارج نطاق هذه المقالة. ومع ذلك، فإنها تشير إلى أنه لكي تكون الشبكة المغزلية ذات معيار غير صفري، يجب استيفاء مطلبين عند كل عقدة. لنفترض أن عقدة تربط ثلاث وحدات بأرقام مغزلية a و b و c. ثم، تذكر هذه المتطلبات على النحو التالي:
معادلة متراجحة (متباينة) المثلث: لا بد أن يكون مجموع أي طرفين من الأطراف الثلاثة للمعادلة أقل من أو يساوي مجموع الطرفين الآخرين. أي أن:
- يجب أن يكون أ ≤ ب (أقل من أو يساوي).
- ب ≤ (أ + ج) (أقل من أو يساوي).
- ج ≤ أ + ب (أقل من أو يساوي).
حفظ الفرميون: يجب أن يكون a + b + c رقما زوجيا.
على سبيل المثال، يكون (أ = 3، ب = 4، ج = 6) مستحيلاً لأن حاصل مجموع الأضلاع الثلاثة (3 + 4 + 6 = 13) هو عدد فردي، ويكون (أ = 3، ب = 4، ج = 9) مستحيلاً لأن 9 أكبر من مجموع الأضلاع الثلاثة (9 > 3 + 4). وفي المقابل فإن (أ = 3، ب = 4، ج = 5) ممكناً لأن مجموع الأضلاع الثلاثة (3 + 4 + 5 = 12) عدد زوجي، ويحقق المتراجحة المثلثية. تستخدم بعض الاتجاهات العلمية ترقيم الأعداد النصفية، شرط أن يكون مجموع الأعداد (أ + ب + ج) عددًا صحيحًا.
التعريف الرسمي للشبكة المغزلية
تُعرَّف الشبكة المغزلية رسميًا على أنها رسم بياني موجه تكون حوافُه مرتبطة بتمثيلات غير قابلة للاختزال لزمرة لي متراصة، وتكون رؤوسُه مرتبطة بالوسائط بين التمثيلات المجاورة على الحواف.
خصائص الشبكة المغزلية
يمكن استخدام الشبكة المغزلية المغمورة في مُتعددَ الشعب (الشتيتة) لتعريف دالة وظيفية على الفضاء المتصل في هذا المُتعدد.
الشبكة المغزلية المغمورة في مُتعددَ الشعب (الشتيتة) يمكن استخدامها لتعريف دالة وظيفية على الفضاء المتصل في هذا المُتعدد، من خلال حساب المرافقات (ترجمة مفترضة ل Holonomies) للاتصال على طول كل رابطة (مسار مغلق) في الرسم البياني، نحسب أولاً مصفوفات التمثيل المقابلة لكل رابطة، ثم نضرب جميع المصفوفات والمتشابكات معًا، وأخيرًا نختزل المؤشرات بطريقة محددة مسبقًا. من أبرز سمات الدالة الوظيفية الناتجة أنها تظل ثابتة تحت نظرية المقياس.
استخدام الشبكة المغزلية في الفيزياء
تمثل الشبكة المغزلية في سياق نظرية الجاذبية الكمية الحلقية وصفاً كموميًا لحقل الجاذبية على السطح الفائق ثلاثي الأبعاد وتكون مجموعة جميع الشبكات المغزلية قابلة للعد؛ وهي تشكل قاعدة فضاء هيلبيرت.
من أهم نتائج نظرية الجاذبية الكمومية الحلقية تكميم المساحات، حيث يكون للعامل المسؤول عن مساحة سطح ثنائي الأبعاد Σ طيف منفصل. وتكون كل شبكة مغزلية حالة خاصة لهذا العامل، وقيمة المنطقة الخاصة بها تساوي:
حيث تُجمع القيمة على جميع التقاطعات i بين السطح Σ والشبكة المغزلية. في هذه الصيغة،
- ℓPL هول طول بلانك,
- معلمة إميرزي و
- ji = 0, 1/2, 1, 3/2, المغزل المرتبط بالرابط i من الشبكة المغزلية. وبالتالي فإن المنطقة ثنائية الأبعاد "تتركز" في التقاطعات مع الشبكة المغزلية.
According to this formula, the lowest possible non-zero eigenvalue of the area operator corresponds to a link that carries spin 1/2 representation. وفقًا لهذه الصيغة، فإن أقل قيمة ذاتية ممكنة غير صفرية لمعلمة المساحة تتوافق مع رابط يحمل تمثيلًا مغزليًا 1/2. بافتراض أن معلمة إميرزي على مستوى 1، فإن هذا يعطي أصغر مساحة ممكنة قابلة للقياس تبلغ حوالي 10^-66 سم^2.
تصبح صيغة قيم المساحة الذاتية أكثر تعقيدًا إذا سُمح للسطح بالمرور عبر الرؤوس (العقد)، كما هو الحال مع نماذج الانتشار الشاذة. كما أن القيم الذاتية لمساحة المعلمة أ مقيدة بالتماثل السلمي.
ينطبق تكميم مماثل على معلمة الحجم. حيث نحصل على حجم الشتيتة الفرعية ثلاثية الأبعاد التي يحتوي على جزء من الشبكة المغزلية من خلال جمع قيمة كل عقدة داخله. يمكن للمرء تصور أن كل عقدة في شبكة مغزلية هي "كمومية حجم" أولية وكل رابط هو "كمومية مساحة" تحيط بهذا الحجم.
الاستخدام في الرياضيات
تستخدم الشبكة المغزلية في الرياضيات لدراسة العقدة الثابتة والفئات المكافئة.
المراجع
- ↑ تعدى إلى الأعلى ل: 1٫0 1٫1 R. Penrose (1971a), "Angular momentum: an approach to combinatorial spacetime," in T. Bastin (ed.), Quantum Theory and Beyond, Cambridge University Press (this paper can be found online on John C. Baez's website); and R. Penrose (1971b), "Applications of negative dimensional tensors," in D. J. A. Welsh (ed.), Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), Academic Press, pp. 221–244, esp. p. 241 (the latter paper was presented in 1969 but published in 1971 according to Roger Penrose, "On the Origins of Twistor Theory" (Archived June 23, 2021) in: Gravitation and Geometry, a Volume in Honour of I. Robinson, Biblipolis, Naples 1987).

